
|
|||||
| the official vFL Journal |
|
||||
|
About the Journal Editorial Board Current issue Instructions for Authors Submit an Article Contact us |
Original Article The Fractal Laboratory Journal 2012;1:2 - ISSN: 2280-3769 (online) STOCHASTIC EFFECTS AND THE LONG-TERM TEMPORAL VARIABILITY OF PSORIASIS SEVERITYStephen Gilmore1 1Dermatology Research Centre, The University of Queensland, School of Medicine, Princess Alexandra Hospital, Brisbane, 4102, AUSTRALIA Submission date: 11 November 2011 Acceptance date: 11 December 2011 Pubblication date: 15 May 2012 ABSTRACT Background The causes of long-term temporal variation in the severity of skin disease - psoriasis in particular - is currently unknown. Here I propose a novel mechanism that can account for such temporal fluctuations in disease severity. Methods Specifically, I suggest that stochastic interaction events between T-cells within the skin associated lymphoid tissue can be amplified to a level where they become clinically manifest. I develop a simple Monte Carlo model that validates the hypothesis but does not prove that the hypothesis is true. Results The model accounts for the coexistence between the generally stable nature of disease on one hand, and the possibility of dramatic and unforeseen exacerbations or remissions on the other, and is able to accurately reproduce severity data derived from a cohort of 800 psoriatic patients tracked for 20 years. Conclusions It is demonstrated that stochastic effects can be amplified to levels that have clinical consequences, and that the variable temporal evolution of disease severity is a necessary consequence of the simple model assumptions. Finally, the ideas presented suggest novel lines of investigation regarding the pathogenesis of psoriasis. BACKGROUND Skin disease is unique among organ specific pathology in the sense that abnormalities are readily visualised. The known long-term temporal variation of severity in many skin diseases - psoriasis in particular - has lead physicians (and patients) to ask the following important question, hitherto unanswered: what are the causes or factors involved in such long-term temporal variation? Are long-term fluctuations in disease severity due to causal factors that remain undetectable, for example microtrauma to the skin in the case of psoriasis, or are they due to something more fundamental? In this paper I focus on psoriasis and suggest that the long-term variation in the severity of clinical disease is indeed due to a fundamental process - stochastic events at the inter-cellular level. To be sure, here I will define inter-cellular stochasticity as the random physical interaction of immunocytes during their passage through the skin-associated-lymphoid tissues [1] (SALT), where the latter may include psoriatic dermis and epiderms [2], unaffected dermis and epidermis, lymph node, or any other relevant lymphoid organ. I note that while the probability of interaction between any given pair of immunocytes cannot be equal, the microscopic dynamics of these interactions will nonetheless proceed in a stochastic manner. Such behaviour is thus analogous to the random motion and interaction of molecules; note that while molecular events occur randomly, macroscopic outcomes, including biochemical processes, occur in a reliable and predictable manner because random events at the molecular level do not occur with equal probability. METHODS To give this hypothesis validity, the problem is therefore reduced to finding a mechanism - represented by a suitable class of models - which can amplify such microscopic random behaviour to a level where it becomes clinically manifest. Three independent observations provide motivation for the development of such a model: first, as noted above, the origins of long-term temporal variability in psoriasis severity remain unknown; second, scientists are now familiar with the notion that stochastic processes may lead to macroscopic effects [3]; and third, a report, unique in scope, provides data over a 20 year period on the severity of psoriasis in a cohort comprising 800 patients, providing a benchmark to which the predictions of any model can be compared [4]. Psoriasis is considered by the majority of investigators to be an example of a T-cell mediated Type-1 inflammatory response [2]. The pathogenic primacy of other classes of cells, including keratinocytes, remains controversial [5]. Nonetheless, the necessity of activated T-cells in the development of the inflammatory plaque is well established [2]. To make a connection between activated T-cells and the severity of psoriasis I assume the average activation level of the relevant circulating immunocytes (likely to be a subset of T-cells) is proportional to psoriasis severity. This assumption, although not proven, is supported by data that demonstrate increased fractions of specific T-cell subsets, including IL-17A+IL-22+IFN γ-cells, in the peripheral blood of patients with psoriasis [6]; the observation that other T-cell subsets, including CD4+CD45RA+ cells, are significantly increased in patients with moderate to severe disease in comparison with patients with mild disease [7]; and the observation that serum IL-22 levels correlate with psoriasis severity [6]. To complete the model requires three more assumptions: first, I define the activation level of an immunocyte as proportional to the cell-surface or intra-cellular concentration of a hypothetical molecule (which I denote by X, and could, for example, represent IL-22); second, I define X as being subject to simple first-order decay; and finally, during an immunocyte interaction event within SALT, I incorporate the idea that the activation status an immunocyte will be incremented in proportion to the activation status of its interacting partner. Incorporating the features above into a Monte Carlo model yields three adjustable parameters: the half-life of X, the activation constant of interacting immunocytes, and the characteristic mixing time - which is defined as the time-scale required for any immunocyte belonging to the relevant subset of T-cells to interact with all others of the same subset.* The symmetric interaction event between any pair (i, j) of immunocytes can be written as a pair of difference equations: xit+1 = xit + axjt - bxit xjt+1 = xjt + axit - bxjt where x denotes the intracellular or cell-surface density of X, a is the activating constant and b is a measure of the half life of X. Implementing the model allows the temporal evolution of the cell-surface or intra-cellular concentration of X to be tracked for an arbitrary number of immunocytes (which I have defined above as belonging to the relevant T-cell subset). RESULTS AND DISCUSSION Fig. 1 shows the evolution of three realizations of the average concentration of X as a function of time (here following the average concentration of X on 100 immunocytes over 10 years) for the following parameter regimes: M > MC(a), M < MC(b), and M = MC(c), where M is the characteristic mixing time defined above. The most striking feature represented in these data is that the system naturally falls into three regimes of dynamical behaviour: first, the situation where the concentration of X is subject to white noise with a well-defined average (a); second, a situation where the concentration of X decays rapidly to zero (b); and finally, an interesting regime where the average concentration of X follows a complicated trajectory (c). In fact, the trajectory (c) is an example of 1/f, or flicker noise [8], and is, in this case, a signature of the system existing near its critical point where a second-order phase transition [9] occurs at T = TC (see Inset, Fig. 2(c)). There are two key features of this latter signal that I hypothesize have implications for the temporal evolution of psoriasis severity: first, the evolution of the average concentration of X has no particular scale, so that fluctuations of any magnitude and for any duration can occur; and second, the system has infinite memory, so that while the recent past will have the greatest influence on the current average concentration of X, events in the distant past may still influence the present. I now run 500 independent 10-year histories where I set T = TC; these simulations are thus equivalent to tracking the temporal evolution of the concentration of X in 100 immunocytes in each of 500 patients. With respect to each realization, since the fluctuations in the concentration of X may occur over short time scales (shorter than the time-scales associated with fluctuations in psoriasis severity) I take its average value over a six-month period as proportional to the severity of psoriasis for that six-month period. Fig. 1(d) and (e) show the results from two such realisations - here I demonstrate results representative of a mildly and severely affected patient respectively. Note how the severity of disease is generally correlated in time, including periods of arbitrary length without disease, yet unexpected dramatic events can occur - for example, Fig. 1(d) shows that a severe exacerbation occurred without warning during the first half of year 7, while Fig 1(e) shows marked and unexpected spontaneous improvement during the second half of year 6. I now compare these results with those of Nijsten et al., where the severity of psoriasis was recorded at four time points in 800 patients over a 20-year period [4]. For the simulations, I specify values for the average concentration of X such that the total fraction of person-years spent without disease, with mild disease, with moderate disease, and with severe disease match the corresponding estimated results from the published study, where the latter are given by 6%, 49%, 33% and 11% respectively. The resultant discriminatory values for the concentration of X turn out to have biological meaning: for example, the value of X that defines the boundary between no disease and mild disease is approximately one percent of the value of X that defines the boundary between moderate and severe disease, implying that the absence of clinical disease corresponds to a profound diminution in the cell-surface or intra-cellular concentration of X. Stratifying the simulated cohort into four severity categories as above at a time point when initial condition bias has been largely removed, I find that the expected likelihood for each category of disease severity at years 1, 5 and 10 correspond well to the reported results derived from the study cohort, where the latter were classified into the same four ordinal groups based on severity at the onset of the study. For example, of all patients with mild disease at the onset of the clinical study, 7%, 53%, 30% and 9% were estimated, respectively, to have none, mild, moderate and severe disease at year 10 [4]. The simulations yield similar results: 7%, 56%, 27% and 11% respectively. Finally, I find that the expected durations (out of 20 years) that patients will spend in each severity category, as a function of their initial severity category, are in good agreement with those generated from the clinical study (Table 1). * For results shown in Figs. 1(a), (b), (c) these dimensional values are given 6, 0.42, and 4 days respectively. Note that these values are biologically plausible. CONCLUSIONS These results allow two important conclusions to be drawn: first, realistic mechanisms can amplify stochastic fluctuations to levels that have clinical consequences; and second, the defining feature of the temporal evolution of psoriasis severity - a coexistence between the stability of severity status on one hand, and the possibility of dramatic and unforseen exacerbations or remissions on the other - is a necessary consequence of the simple model assumptions. Does this hypothesis suggest any novel investigations? The dynamical behaviour of the model rests on the notion that T-cells of a similar or identical phenotype can self-interact; that is, the ability of a T-cell to activate another T-cell of the same phenotype. To identify potential important subsets of T-cells in psoriasis, it may therefore be beneficial to investigate a variety of T-cell subsets in vitro, with the aim of identifying particular subsets capable of self-interaction and activation. Finally, the critical dynamics inherent in the hypothesis - crucial in reproducing clinical behaviour - suggests that the long-term monitoring of cohorts of psoriatic individuals with respect to T-cell cell-surface or intracellular lymphokine concentrations may yield results that demonstrate the existence of time-dependent scale-invariant or fractal signals. REFERENCES 1. Streilein JW: Circuits and signals of the Skin-Associated- Lymphoid-Tissues (SALT). J Invest Dermatol 1985, 85: 10s-13s. 2. Lew W, Bowcock AM, Kreuger JG: Psoriasis vulgaris: cutaneous lymphoid tissue supports T-cell activation and 'Type-1' inflammatory gene expression. Trends Immunol 2004, 25: 295-305. 3. Sagues F, Sancho J, Garcis-Ojalvo J: Spatiotemporal order out of noise. Rev Mod Phys 2007, 79: 829-882. 4. Nijsten T, Looman C, Stern R: Clinical severity of psoriasis in last 20 years of PUVA study. Arch Dermatol 2007, 143: 1113-1121. 5. Sano S, Chan KS, Carbajal S, Clifford J, Peavey M, Kiguchi K et al. Stat3 links activated keratinocytes and immunocytes required for development of psoriasis in a novel transgenic mouse model. Nat Med 2005, 11: 43-49. 6. Kagami S, Rizzo HL, Lee JJ, Koguchi Y, Blauvelt A: Circulating Th17, Th22 and Th1 cells are increased in psoriasis. J Invest Dermatol 2010, 130(5): 1373-1383. 7. Langewouters AMG, van Erp PEJ, de Jong EMGJ, ven de Kerhof PCM: Lymphocyte subsets in peripheral blood of patients with moderate-to-severe versus mild plaque psoriasis. Arch Dermatol Res 2008, 300: 107-113. 8. Gisiger T: Scale invariance in biology: coincidence or footprint of a universal mechanism? Biol Rev, 2001, 76: 161-209. 9. Ward M: Universality. London: Pan Macmillan; 2001. FIGURES Figure 1 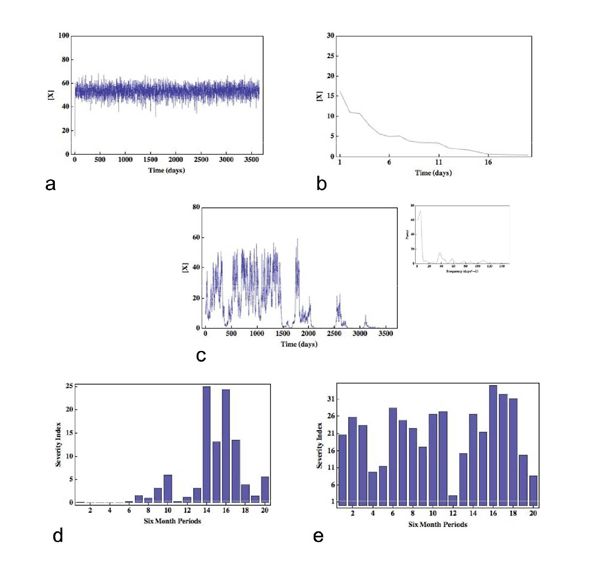
Fig. 1. An example of the variation in average density of X for three parameter regimes (a), (b), (c), and in the psoriasis severity index for mild (d) and moderate to severe disease (e). For m = 0.26 the signal has a well-defined mean which is subject to white noise (a) while for m = 0.245 the cell-surface density of X rapidly decays to zero (b). At m = 0.24975 the signal demonstrates significant temporal fluctuations and is an example of 1/f noise occurring at the phase transition. A plot of the power spectrum (Inset) shows that the power decays inversely with frequency (in this case the calculated exponent is -1.1). Note that in (c) there are prolonged periods associated with very different values for the cell-surface density or intracellular concentration of X, and that fluctuations of all sizes occur. In (d), a representative evolution of mild disease over a 10-year period is shown, while (e) is representative of a more severely affected patient. TABLES Table 1. Expected number of years (of a total of 20) patients will spend in each psoriasis severity category, as a function of initial severity. Values in parentheses are taken from Ref. [4] with permission.
|